

AI智能文摘
暂无文摘

背景
前面提到的 casino 数值模型时,涉及到了马可夫链相关的信息,有朋友在后台问了些马可夫链的使用方法,我当时回答的不是很清楚。所以,这里继续进行探讨下马可夫链在赌场老虎机(casino slots)中的应用。
本文通过马可夫链建模和计算,来理解老虎机的状态转移过程以及长期期望收益,涉及的内容包括:马可夫链,老虎机,赌场,概率论,状态转移矩阵,稳态分布,长期期望收益等等。Ps:我个人认为最重要的就是状态转移的思想,其他都是次要的。
• 通过一些简单的例子,展示如何使用马可夫链理论来预测老虎机的回报率。
• 通过一些简单的例子,计算特定符号组合的长期出现概率,并评估各种策略的有效性。
• 通过更深入的数学分析和计算实例,为读者提供了一个理解和优化老虎机游戏的框架。
全文一共 4000 字,阅读大概需要 18 分钟,让我们开始吧。
回顾
赌场老虎机是世界上最受欢迎的赌博游戏之一,其背后的数学原理使得游戏充满了随机性和不可预测性。马可夫链作为一种数学模型,能够有效地描述老虎机游戏中符号组合的状态转移过程。通过马可夫链,我们可以分析老虎机在长期运行中的行为,预测每个状态的长期出现概率,以及计算玩家的预期收益。
本论文将首先回顾马可夫链的基本理论,然后探讨其在老虎机中的应用。我们将通过多个详细的数学实例,展示如何利用马可夫链模型来分析和优化老虎机游戏。
马可夫链理论概述
马可夫链定义
马可夫链是一种用于描述一个系统在不同状态之间随机转移的数学模型。其关键特点是“无后效性”(Markov property),即系统的未来状态只取决于当前状态,而与过去的状态无关。这使得马可夫链特别适合用于建模一系列随机事件,例如老虎机的符号组合变化。
一个离散时间马可夫链由以下几个要素构成:
• 状态空间 S:所有可能状态的集合,记为 S={s1,s2,…,sn}。
• 转移概率矩阵 P:一个 n×n 的矩阵,其中每个元素 Pij 表示系统从状态 si 转移到状态 sj 的概率。
• 初始状态分布 π0:表示系统在初始时刻位于各状态的概率分布。
马可夫链的分类
马可夫链可分为齐次马可夫链和非齐次马可夫链。齐次马可夫链的转移概率在时间上是恒定的,即 P(t)=P 对所有 t 都成立;而非齐次马可夫链的转移概率矩阵会随着时间的变化而变化。在赌场老虎机的应用中,通常假设马可夫链是齐次的,因为老虎机的随机数生成机制通常是时间无关的。
稳态分布
稳态分布是指在长时间运行后,系统达到的一种平衡状态,在这种状态下,每个状态的概率不再随时间变化。稳态分布 π 满足以下方程:πP = π
其中, π 是一个行向量,表示系统在各个状态的长期概率分布。稳态分布的存在性和唯一性通常依赖于马可夫链的性质,如是否为不可约(irreducible)和遍历(ergodic)。
马可夫链在赌场老虎机中的应用
老虎机的基本原理
老虎机是一种通过随机数生成器(RNG)来决定符号组合的赌博设备。每个转轮上都有若干个符号,玩家通过拉动拉杆或按下按钮来启动转轮,最终形成的符号组合决定玩家的输赢。老虎机的概率特性可以通过马可夫链建模,以分析其状态转移过程和长期收益。
老虎机模型的马可夫链构建
假设我们分析一个简单的老虎机模型,具有三个转轮,每个转轮上有三个符号 S={A,B,C}。每个转轮独立地停在这三个符号之一上,因此整个系统的状态空间可以表示为所有可能的符号组合 (X1,X2,X3),其中 Xi∈S。
在这个例子中,状态空间的大小为 ∣S∣3=27,即27种可能的符号组合。每种状态的转移概率可以通过以下方式计算:由于每个转轮独立且等概率地停在某个符号上,任意两个状态之间的转移概率为:
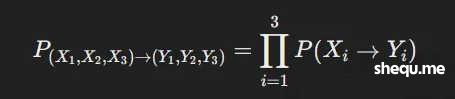
对于每个 i,P(Xi→Yi)=1/3,因此整个状态转移概率矩阵 P 是一个 27×27 的矩阵,其中每个元素等于 1/27。
实例1:长期期望收益的计算
假设某个老虎机的奖金规则如下:
• 符号组合 (A,A,A) 奖金为100元
• 符号组合 (B,B,B) 奖金为50元
• 符号组合 (C,C,C) 奖金为25元
• 其他组合不支付奖金
根据状态转移矩阵,我们可以计算出每个符号组合的长期概率(即稳态分布)。由于每个状态的转移概率相等,因此稳态分布为均匀分布,每个状态的概率为 1/27。
长期期望收益 E 为所有符号组合收益的加权平均值:
E=∑i=1/27 × πi × 奖金i =1/27×(100+50+25)=6.48元
这意味着在无限多次游戏后,玩家平均每次游戏的期望收益为6.48元。
实例2:符号组合的出现概率
除了计算长期期望收益,马可夫链还可以用于计算特定符号组合在长期运行中的出现概率。假设我们关注符号组合 (A,B,C)的出现概率。
在前面的假设中,由于每个状态的长期概率均为 1/27,因此组合 (A,B,C) 的出现概率为 1/27。然而,在更复杂的老虎机设计中,不同符号的出现概率可能不同。例如,如果符号 A 的出现概率为 pA=0.5,符号 B 和 C 的出现概率为 pB=0.3 和 pC=0.2,那么我们可以构建一个非均匀分布的转移概率矩阵。
在这种情况下,组合 (A,B,C) 的出现概率为:
P(A,B,C)=pA×pB×pC=0.5×0.3×0.2=0.03
这种计算能够帮助赌场设计更复杂的老虎机,并预测不同符号组合的出现频率。
实例3:策略优化与收益分析
赌场运营商可以利用马可夫链分析,优化老虎机的设计和奖金分配策略。例如,假设赌场希望设计一种老虎机,使得特定组合 (A,A,A) 的出现概率极低,但其对应的奖金极高。通过调整符号的出现概率 pA,可以直接影响这一组合的长期概率。
如果符号 A 的出现概率降至 pA=0.1,那么组合 (A,A,A) 的出现概率将变为:
P(A,A,A)=(0.1)3=0.001
即每1000次游戏才可能出现一次。然而,由于这一组合的稀有性,赌场可以设置一个极高的奖金,例如1000美元。玩家可能被这种高奖金吸引,而赌场则通过其他更常出现的低奖金组合来平衡支付。
通过计算不同策略下的长期期望收益,赌场可以优化老虎机的设计,以确保既能吸引玩家又能实现预期的盈利目标。
数学分析与进一步讨论
马可夫链中的重要概念
在分析老虎机时,以下几个马可夫链的概念尤为重要:
• 不可约性:如果每个状态都可以通过若干步到达另一个状态,则马可夫链是不可约的。对于老虎机,这意味着任意一个符号组合在足够多次拉杆后都可能出现。
• 遍历性:如果一个状态是不可约且递归的,则称为遍历状态。对于老虎机模型,遍历性意味着每个符号组合在长期运行中都会多次出现,并且其出现频率符合稳态分布。
• 周期性:如果状态的转移具有固定的周期性,则马可夫链具有周期性。在设计老虎机时,通常希望避免周期性,以确保符号组合的出现是随机的。
数值计算与模拟
在实际应用中,计算马可夫链的稳态分布和期望收益通常需要数值模拟。通过计算大量的拉杆结果,赌场可以估计符号组合的长期出现概率和期望收益。此外,现代老虎机中广泛应用的随机数生成器也可以通过马可夫链模型进行验证和优化。
例如,通过蒙特卡罗模拟方法,我们可以反复模拟数百万次拉杆,记录每次符号组合的结果,进而估计每个状态的长期概率。这种方法特别适用于符号组合数目庞大且转移概率复杂的老虎机。
参数调整与敏感性分析
马可夫链模型的另一个重要应用是参数调整与敏感性分析。通过调整符号的出现概率或转移规则,赌场可以测试不同策略对期望收益和玩家体验的影响。
例如,考虑增加一个新的符号 D,并设置其出现概率为 pD=0.05。我们可以构建新的转移概率矩阵,重新计算稳态分布和期望收益,分析这一变化对整个系统的影响。如果新增的符号组合能够提高玩家的期望收益或增强游戏的吸引力,赌场可能会考虑实施这一变化。另一方面,如果符号 D 的出现概率过高,可能会导致期望收益降低,从而影响赌场的盈利能力。因此,参数调整与敏感性分析能够帮助赌场运营商在设计老虎机时做出更加明智的决策。
多重状态转移与复杂老虎机
在更加复杂的老虎机中,可能存在多个独立的状态转移过程。例如,有的老虎机具有多个游戏阶段,每个阶段对应不同的符号组合和转移概率。为了分析这些复杂的老虎机设计,可以使用扩展的马可夫链模型,即考虑一个由多重子状态空间组成的状态空间。
假设一个老虎机具有两个游戏阶段,每个阶段的符号组合分别为 S1={A,B,C} 和 S2={D,E,F}。每个阶段之间的转移可以用一个子状态转移矩阵来表示,而整个系统的状态转移矩阵则是这两个子状态矩阵的张量积。
例如,考虑阶段一的状态转移矩阵 P1 和阶段二的状态转移矩阵 P2 :
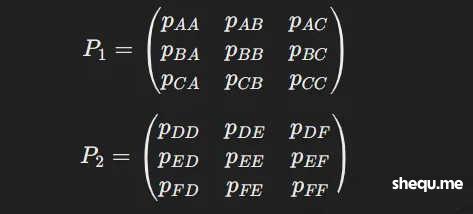
整个系统的状态转移矩阵 P 可以通过 P1 和 P2 的张量积计算得出。这样,我们可以分析不同阶段之间的状态转移过程,计算整个系统的稳态分布,并进一步预测玩家在不同阶段的预期收益。
案例研究:复合型老虎机的收益分析
为进一步说明上述理论的应用,考虑一个复合型老虎机案例。假设老虎机由三个阶段组成,每个阶段都有不同的符号和转移概率,并且每个阶段之间的转移概率也不同。
• 阶段一:符号组合 {A,B,C},初始转移概率 P1。
• 阶段二:符号组合 {D,E,F},转移概率矩阵 P2。
• 阶段三:符号组合 {G,H,I},转移概率矩阵 P3。
玩家首先在阶段一中进行游戏,并根据符号组合的结果决定是否进入阶段二或直接结束游戏。如果进入阶段二,玩家将继续根据符号组合的结果进入阶段三或结束游戏。假设每个阶段的符号组合出现概率和奖金规则如下:
• 阶段一:符号 AAA, BBB, CCC 分别对应奖金 10, 20, 30 元;
• 阶段二:符号 DDD, EEE, FFF 分别对应奖金 40, 50, 60 元;
• 阶段三:符号 GGG, HHH, III 分别对应奖金 70, 80, 90 元。
通过马可夫链模型,我们可以计算出每个阶段的符号组合出现概率,继而计算玩家在每个阶段的期望收益。最终的期望收益为所有阶段收益的加权和。这样赌场运营商可以分析复合型老虎机的整体盈利能力,并根据玩家行为优化各阶段的设计和奖金分配。
结论
在本文中,我们探讨了马可夫链在赌场老虎机中的应用,特别是如何通过马可夫链模型来分析老虎机的状态转移过程、计算长期期望收益以及评估不同设计策略的有效性。通过多个具体的数学实例,我们展示了马可夫链模型如何帮助赌场运营商优化老虎机设计,并为玩家提供数学依据,以制定更为理性的游戏策略。
马可夫链为复杂的老虎机系统提供了强大的分析工具,尤其是在现代赌场中,老虎机设计日益复杂,涉及多个游戏阶段和符号组合。在未来的研究中,进一步探索马可夫链的变体(如部分可观察的马可夫链、非齐次马可夫链)在更复杂的老虎机模型中的应用,将是一个具有挑战性且富有潜力的方向。

参考文献
1. Ross, S. M. (2014). Introduction to Probability Models. Academic Press.
2. Norris, J. R. (1997). Markov Chains. Cambridge University Press.
3. Sheldon, R. (2013). The Mathematics of Games: An Introduction to Probability. CRC Press.
4. Ethier, S. N. (2010). The Doctrine of Chances: Probabilistic Aspects of Gambling. Springer.
5. Grimmett, G., & Stirzaker, D. (2001). Probability and Random Processes. Oxford University Press.
6. Kemeny, J. G., Snell, J. L., & Knapp, A. W. (1976). Denumerable Markov Chains. Springer.






 欢迎来到赌狗吧
欢迎来到赌狗吧